
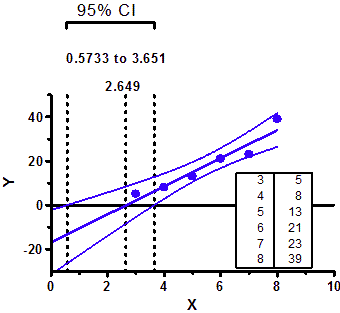
The curve on this graph plots the predicted probability of passing the test (Y) as a function of the number of hours studied (X). This graph (shown below), confirms some of the observations that we made in the previous sections: If we break away from the results sheet for just a moment, we can take a look at the curve that logistic regression plotted for our data. Probability of success = 0.797 or 79.7% The logistic regression curve Odds = 3.934 = (Probability of success)/(1 - Probability of success)ģ.934*(1 - Probability of success) = Probability of successģ.934 - 3.934*(Probability of success) = Probability of successģ.934 = Probability of success + 3.934*(Probability of success)ģ.934 = (Probability of success)*(1 + 3.934) It is easy to convert this odds to a probability: That is the predicted odds of passing for students that studied 4.37 hours (just one hour extra). Thus, increasing X by 1, from 3.37 to 4.37 gives us a new odds of 1*3.934, or just 3.934. We know that the odds are 1 when X is 3.37, and the odds ratio is 3.934. Remember, the odds ratio that Prism reports tells us by how much the odds are multiplied when X increases by 1. If we combine this result with the odds ratio, we can quickly determine the odds and probability of passing if the student studies one hour more. In our case, the value of X at 50% is 3.37, meaning that for those students that studied 3.37 hours, the odds of passing the test were 1:1 (a 50% probability of passing. Interestingly, using our equation for odds given above, we can see that when probability is 50%, the odds are equal to 1 (also known as "even odds"). X at 50%Īnother key value that Prism reports for simple logistic regression is the value of X when the probability of success is predicted to be 50% (or 0.5). Odds = (Probability of success)/(1 - Probability of success)įor example, let's say there's a 75% probability of success, the odds would then be calculated as:Ĭommonly, we would say that "the odds are 3:1" (read "three to one"). Since the probability of failure is just 1 - Probability of success, we can write this as: Odds = Probability of success/Probability of failure In case you haven't read about the relationship of probability and odds, here's a quick summary:
Thus, an odds ratio of 3.934 tells us that for every additional hour studied, the odds of passing the test are multiplied by almost 4! Recall that X represents the number of hours studied. Take the values in these results, for example. Odds ratiosīecause it is hard to directly interpret β0 and β1, it's common to look instead to the odds ratios and their 95% confidence intervals (reported farther down on the results sheet).Ī more detailed explanation of odds ratios can be found here, but what the odds ratio for β1 tells us is that increasing X by 1 multiplies the odds of success by the value for β1. These parameters are sometimes referred to as the "intercept" and "slope", respectively, based on their relationship to the "log odds". The first thing that you'll see on the results sheet are the best fit value estimates along with standard errors and 95% confidence intervals for both β0 and β1. Results of simple logistic regression Parameter estimates Once you click "OK", you'll be taken to the main results sheet which will be discussed in the next section.

The results for some of these options are discussed below, but additional information can for these options can be found here. For the purposes of this walkthrough, we won't need to change any of the default options. Alternatively, you can click on the "Analyze" button in the toolbar, then select "Simple logistic regression" from the list of available XY analyses.Īfter clicking the simple logistic regression button, the parameters dialog for this analysis will appear. To perform simple logistic regression on this dataset, click on the simple logistic regression button in the toolbar (shown below). This data represents a collection of 125 students and the amount of time that they spent preparing for a test along with the outcome of the test: did the student pass (entered as a 1 in the data table) or did the student fail (entered as a 0 in the data table)? Initiating the analysis You will then be shown a set of data with two columns: "Hours Studied" in the X column and "Test Passed?" in the Y column. To use this data, click on "Simple logistic regression" in the list, and then click "Create".
To begin, we'll want to create a new XY data table from the Welcome dialogįor the purposes of this walkthrough, we will be using the Simple logistic regression sample data found in the "Correlation & regression" section of the sample files. Logistic regression was added with Prism 8.3.0 The data This guide will walk you through the process of performing simple logistic regression with Prism.


 0 kommentar(er)
0 kommentar(er)
